例如中国婚庆糖果网有大量用户的网站，用户拥有积分，积分可能会在使用过程中随时 更新。现在要为该网站设计⼀一种算法，在每次用户登录时显示其 当前积分排名。用户大规模为2亿;积分为非负整数，且小于 100万。

存储结构

首先，我们用⼀一张用户积分表user_score来保存用户的积分信息。

表结构：

示例数据：

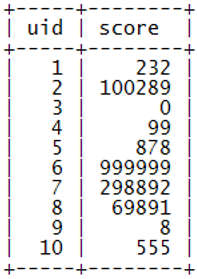
下面的算法会基于这个基本的表结构来进行。

算法1：简单SQL查询 首先，我们很容易想到用⼀一条简单的SQL语句查询出积分大于该用户积分的用户数量：

select 1 + count(t2.uid) as rank from user_score t1, user_score t2 where t1.uid = @uid and t2.score > t1.score

对于4号用户我们可以得到下面的结果：

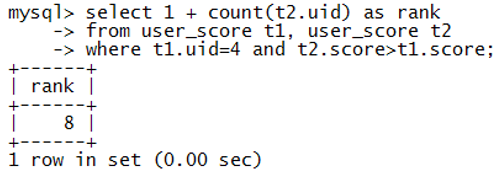
算法特点

优点：简单，利用了SQL的功能，不需要复杂的查询逻辑，也不引入额外的存储结构，对小规模或性能要求不高的应用不失为⼀一 种良好的解决方案。

缺点：需要对user_score表进行全表扫描，还需要考虑到查询的 同时若有积分更新会对表造成锁定，在海量数据规模和高并发的 应用中，这样做性能是无法接受的。

算法2：均匀分区设计

在许多应用中缓存是解决性能问题的重要途径，我们自然会想：

能不能把用户排名用Memcached缓存下来呢?不过再⼀一想发现 缓存似乎帮不上什么忙，因为用户排名是⼀一个全局性的统计指 标，而并非用户的私有属性，其他用户的积分变化可能会马上影 响到本用户的排名。然而，真实的应用中积分的变化其实也是有 ⼀一定规律的，通常⼀一个用户的积分不会突然暴增暴减，⼀一般用户 总是要在低分区混迹很长⼀一段时间才会慢慢升入高分区，也就是 说用户积分的分布总体说来是有区段的，我们进⼀一步注意到高分 区用户积分的细微变化其实对低分段用户的排名影响不大。于 是，我们可以想到按积分区段进行统计的方法，引入⼀一张分区积 分表score_range：

表结构：

数据示例：

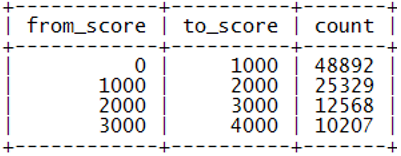
表示[from_score, to_score)区间有count个用户。若我们按每 1000分划分⼀一个区间则有[0, 1000), [1000, 2000), …, [999 000, 1 000 000)这1000个区间，以后对用户积分的更新要相应地更新 score_range表的区间值。在分区积分表的辅助下查询积分为s的 用户的排名，可以首先确定其所属区间，把高于s的积分区间的 count值累加，然后再查询出该用户在本区间内的排名，二者相 加即可获得用户的排名。

乍一看，这个方法貌似通过区间聚合减少了查询计算量，实则不然。大的问题在于：如何查询用户在本区间内的排名呢?如果是在算法1中的SQL中加上积分条件：

select 1 + count(t2.uid) as rank from user_score t1, user_score t2 where t1.uid = @uid and t2.score > t1.score and t2.score < @to_score

在理想情况下，由于把t2.score的范围限制在了1000以内，如果 对score字段建立索引，我们期望本条SQL语句将通过索引大大 减少扫描的user_score表的行数。不过真实情况并非如此， t2.score的范围在1000以内并不意味着该区间内的用户数也是 1000，因为这里有积分相同的情况存在!二八定律告诉我们， 前20%的低分区往往集中了80%的用户，这就是说对于大量低分 区用户进行区间内排名查询的性能远不及对少数高分区用户进行 排名查询，所以在⼀一般情况下这种分区方法不会带来实质性的性 能提升。

算法特点

优点：注意到了积分区间的存在，并通过预先聚合消除查询的全 表扫描。

缺点：积分非均匀分布的特点使得性能提升并不理想。

算法3：树形分区设计

均匀分区查询算法的失败是由于积分分布的非均匀性，那么我们 自然就会想，能不能按二八定律，把score_range表设计为非均 匀区间呢?比如，把低分区划密集⼀一点，10分⼀一个区间，然后逐 渐变成100分，1000分，10 000分 …… 当然，这不失为⼀一种方 法，不过这种分法有⼀一定的随意性，不容易把握好，而且整个系 统的积分分布会随着使用而逐渐发生变化，初的较好的分区方 法可能会变得不适应未来的情况了。我们希望找到⼀一种分区方 法，既可以适应积分非均匀性，又可以适应系统积分分布的变 化，这就是树形分区。 我们可以把[0, 1 000 000)作为⼀一级区间;再把⼀一级区间分为两 个2级区间[0, 500 000), [500 000, 1 000 000)，然后把二级区间 二分为4个3级区间[0, 250 000), [250 000, 500 000), [500 000, 750 000), [750 000, 1 000 000)，依此类推，终我们会得到1 000 000个21级区间[0,1), [1,2) … [999 999, 1 000 000)。这实际 上是把区间组织成了⼀一种平衡二叉树结构，根结点代表⼀一级区 间，每个非叶子结点有两个子结点，左子结点代表低分区间，右 子结点代表高分区间。树形分区结构需要在更新时保持⼀一种不变 量(Invariant)：非叶子结点的count值总是等于其左右子结点的 count值之和。

虽然，本算法的更新和查询都涉及若干个操作，但如果我们为区 间的from_score和to_score建立索引，这些操作都是基于键的查 询和更新，不会产生表扫描，因此效率更高。另外，本算法并不依赖于关系数据模型和SQL运算，可以轻易地改造为NoSQL等 其他存储方式，而基于键的操作也很容易引入缓存机制进⼀一步优 化性能。进⼀一步，我们可以估算⼀一下树形区间的数目大约为200 000 000，考虑每个结点的大小，整个结构只占用几十M空间。 所以，我们完全可以在内存建立区间树结构，并通过user_score 表在O(n)的时间内初始化区间树，然后排名的查询和更新操作都 可以在内存进行。⼀一般来讲，同样的算法，从数据库到内存算法 的性能提升常常可以达到105以上;因此，本算法可以具有非常 高的性能。

算法特点

优点：结构稳定，不受积分分布影响;每次查询或更新的复杂度 为积分大值的O(log n)级别，且与用户规模无关，可以应对海 量规模;不依赖于SQL，容易改造为NoSQL或内存数据结构。

缺点：算法相对更复杂。

算法4：积分排名数组

算法3虽然性能较高，达到了积分变化的O(log n)的复杂度，但 是实现上比较复杂。另外，O(log n)的复杂度只在n特别大的时 候才显出它的优势，而实际应用中积分的变化情况往往不会太 大，这时和O(n)的算法相比往往没有明显的优势，甚至可能更 慢。

考虑到这⼀一情况，仔细观察⼀一下积分变化对排名的具体影响，可 以发现某用户的积分从s变为s+n，积分小于s或者大于等于s+n 的其他用户排名实际上并不会受到影响，只有积分在[s, s+n)区 间内的用户排名会下降1位。我们可以用⼀一个大小为100 000 000 的数组表示积分和排名的对应关系，其中rank[s]表示积分s所对 应的排名。初始化时，rank数组可以由user_score表在O(n)的复 杂度内计算而来。用户排名的查询和更新基于这个数组来进行。 查询积分s所对应的排名直接返回rank[s]即可，复杂度为O(1); 当用户积分从s变为s+n，只需要把rank[s]到rank[s+n-1]这n个元 素的值增加1即可，复杂度为O(n)。

算法特点。

优点：积分排名数组比区间树更简单，易于实现;排名查询复杂 度为O(1);排名更新复杂度O(n)，在积分变化不大的情况下非常 高效。

缺点：当n比较大时，需要更新大量元素，效率不如算法3。

总结

上面介绍了用户积分排名的几种算法，算法1简单，易于理解和 实现，适用于小规模和低并发应用;算法3引入了较复杂的树形 分区结构，但是O(log n)的复杂度性能优越，可以应用于海量规 模和高并发;算法4采用简单的排名数组，易于实现，在积分变 化不大的情况下性能不亚于算法3。本问题是⼀一个开放性的问 题，相信⼀一定还有其他优秀的算法和解决方案

本文仅限内部技术人员查阅学习交流,不得作于其他商业用途.原创文章出自:南昌网站建设公司-百恒网络 http://www.jxbh.cn 此文禁止转载,谢谢合作!